15.4 Data transformations
Here we learn how to transform numeric variables using two common methods:
- log-transform
- logit-transform
There are many other types of transformations that can be performed, some of which are described in Chapter 13 of the course text book.
Contrary to what is suggested in the text, it is better to use the “logit” transformation rather than the “arcsin square-root” transformation for proportion or percentage data, as described in this article by Warton and Hui (2011).
15.4.1 Log-transform
When one observes a right-skewed frequency distribution, as seen here in the marine biomass ratio data, a log-transformation often helps.
marine %>%
ggplot(aes(x = biomassRatio)) +
geom_histogram(binwidth = 0.5, color = "black", fill = "lightgrey",
boundary = 0, closed = "left") +
xlab("Biomass ratio") +
ylab("Frequency") +
theme_bw()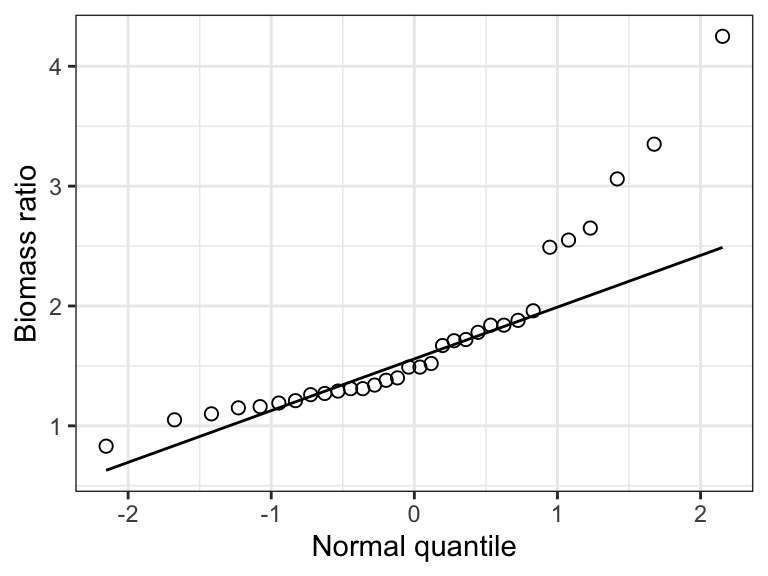
Figure 15.4: The frequency distribution of the ‘biomass ratio’ of 32 marine reserves.
To log-transform the data, simply create a new variable in the dataset using the mutate function (from the dplyr package) that we’ve seen before. Here we’ll call our new variable logbiomass, and use the log function to take the natural log of the “biomassRatio” variable.
We’ll assign the output to the same, original “tibble” called “marine”:
Alternatively, you could use this (less tidy) code to get the same result:
marine$logbiomass <- log(marine$biomassRatio)If your variable includes zeros, then you’ll need to take extra steps, as described in the next section.
Let’s look at the tibble now:
## # A tibble: 32 × 2
## biomassRatio logbiomass
## <dbl> <dbl>
## 1 1.34 0.2927
## 2 1.96 0.6729
## 3 2.49 0.9123
## 4 1.27 0.2390
## 5 1.19 0.1740
## 6 1.15 0.1398
## 7 1.29 0.2546
## 8 1.05 0.04879
## 9 1.1 0.09531
## 10 1.21 0.1906
## # ℹ 22 more rowsNow let’s look at the histogram of the log-transformed data:
marine %>%
ggplot(aes(x = logbiomass)) +
geom_histogram(binwidth = 0.25, color = "black", fill = "lightgrey",
boundary = -0.25) +
xlab("Biomass ratio (log-transformed)") +
ylab("Frequency") +
theme_bw()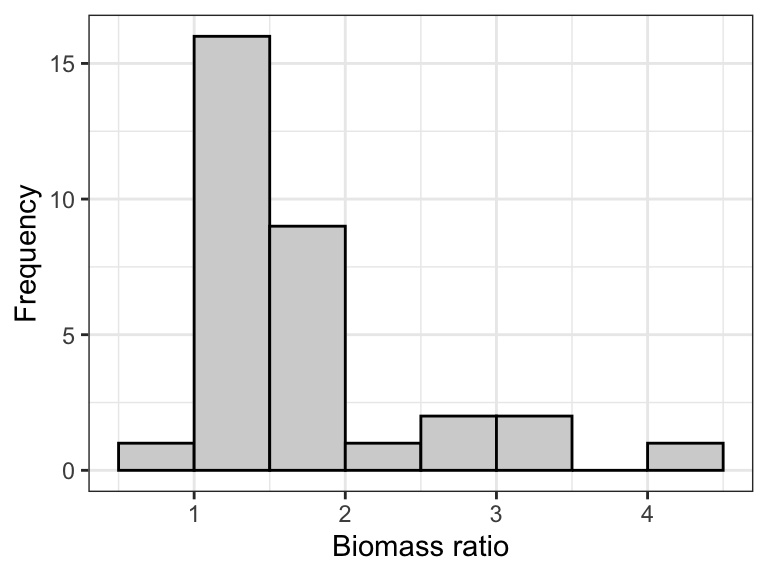
Figure 15.5: The frequency distribution of the ‘biomass ratio’ of 32 marine reserves (log-transformed).
Now the quantile plot:
marine %>%
ggplot(aes(sample = logbiomass)) +
stat_qq(shape = 1, size = 2) +
stat_qq_line() +
ylab("Biomass ratio (log)") +
xlab("Normal quantile") +
theme_bw()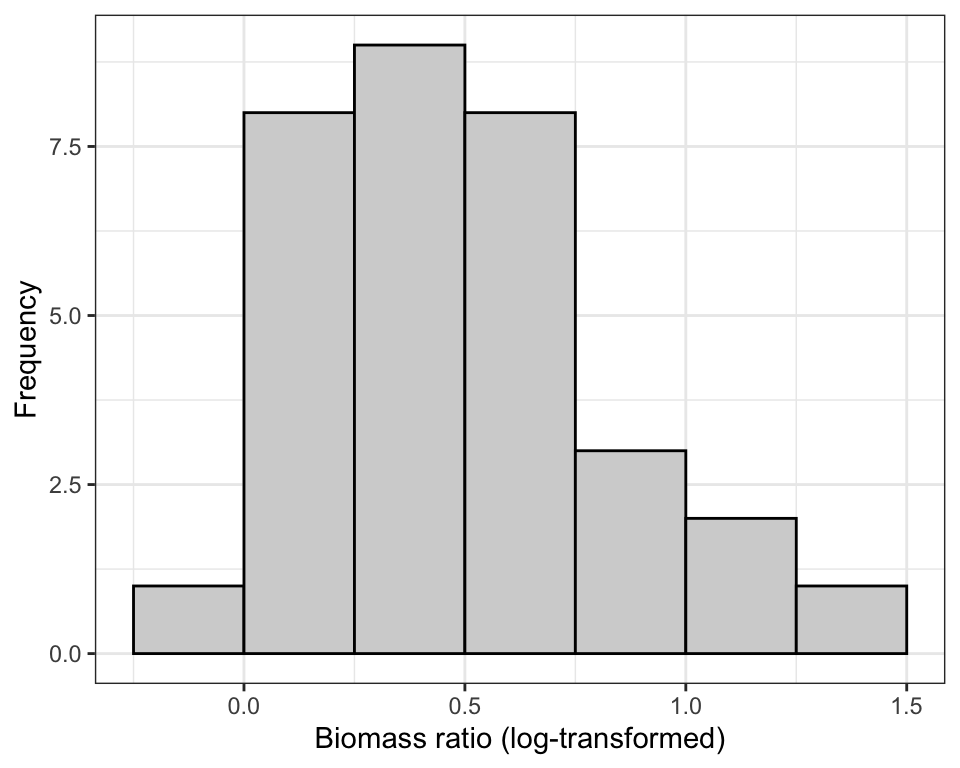
Figure 15.6: Figure: Normal quantile plot of the ‘biomass ratio’ of 32 marine reserves (log-transformed).
The log-transform definitely helped, but the distribution still looks a bit wonky: several of the points are quite far from the line.
Just to be sure, let’s conduct a Shapiro-Wilk test, using an \(\alpha\) level of 0.05, and remembering to tidy the output:
shapiro.log.result <- shapiro.test(marine$logbiomass)
shapiro.log.result.tidy <- tidy(shapiro.log.result)
shapiro.log.result.tidy## # A tibble: 1 × 3
## statistic p.value method
## <dbl> <dbl> <chr>
## 1 0.9380 0.06551 Shapiro-Wilk normality testThe P-value is greater than 0.05, so we’d conclude that there’s no evidence against the assumption that these data come from a normal distribution.
For this example a reasonable statement would be:
Based on the normal quantile plot (Fig. 18.9), and a Shapiro-Wilk test, we found no evidence against the normality assumption (Shapiro-Wilk test, W = 0.94, P-value = 0.066).
You could now proceed with the statistical test (e.g. one-sample t-test) using the transformed variable.
15.4.2 Dealing with zeroes
If you try to log-transform a value of zero, R will return a -Inf value.
In this case, you’ll need to add a constant (value) to each observation, and convention is to simply add 1 to each value prior to log-transforming.
In fact, you can add any constant that makes the data conform best to the assumptions once log-transformed. The key is that you must add the same constant to every value in the variable.
You then conduct the analyses using these newly transformed data (which had 1 added prior to log-transform), remembering that after back-transformation (see below), you need to subtract 1 to get back to the original scale.
Example code showing how to check for zeroes
We’ll create a dataset to work with called “apples”.
Don’t worry about learning this code…
set.seed(345)
apples <- as_tibble(data.frame(biomass = rlnorm(n = 14, meanlog = 1, sdlog = 0.7)))
apples$biomass[4] <- 0Here’s the resulting dataset, which includes a variable “biomass” that would benefit from log-transform:
## # A tibble: 14 × 1
## biomass
## <dbl>
## 1 1.569
## 2 2.235
## 3 2.428
## 4 0
## 5 2.593
## 6 1.745
## 7 1.420
## 8 9.003
## 9 8.657
## 10 9.654
## 11 10.04
## 12 1.020
## 13 1.500
## 14 3.397Here’s a quantile plot of the biomass variable:
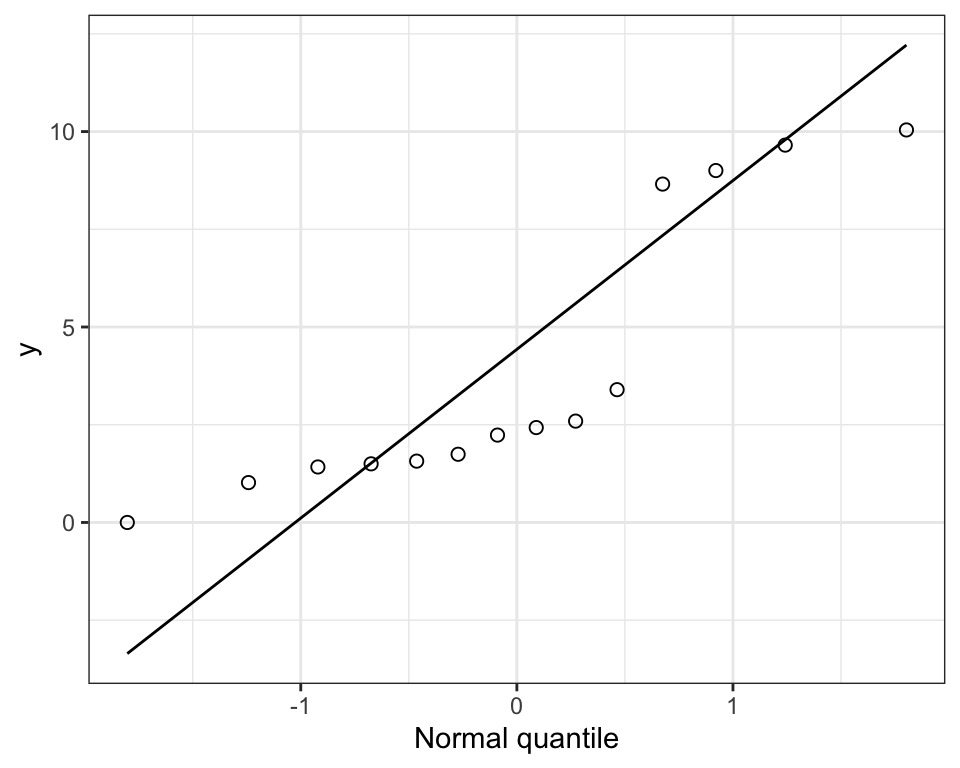
Figure 15.7: Normal quantile plot of made-up biomass data.
Let’s first see what happens when we try to log-transform the “biomass” variable:
## [1] 0.45056428 0.80433995 0.88697947 -Inf 0.95272789 0.55653572
## [7] 0.35059322 2.19753971 2.15833805 2.26733776 2.30674058 0.02011719
## [13] 0.40525957 1.22291473Notice we get a “-Inf” value.
The following code tallies the number of observations in the “biomass” variable that equal zero.
If this sum is greater than zero, then you’ll need to add a constant to all observations when transforming.
## [1] 1So we have one value that equals zero.
So let’s add a 1 to each observation during the process of log-transforming:
Notice that we name the new variable “logbiomass_plus1” in a way that indicates we’ve added 1 prior to log-transforming, and that in the log calculation we’ve used “biomass + 1”.
Let’s see the result:
## # A tibble: 14 × 2
## biomass logbiomass_plus1
## <dbl> <dbl>
## 1 1.569 0.9436
## 2 2.235 1.174
## 3 2.428 1.232
## 4 0 0
## 5 2.593 1.279
## 6 1.745 1.010
## 7 1.420 0.8837
## 8 9.003 2.303
## 9 8.657 2.268
## 10 9.654 2.366
## 11 10.04 2.402
## 12 1.020 0.7033
## 13 1.500 0.9162
## 14 3.397 1.481Notice that we still have a zero in the newly created variable, AFTER having transformed, because for that value we calculated the log of “1” (which equals zero). That’s OK!
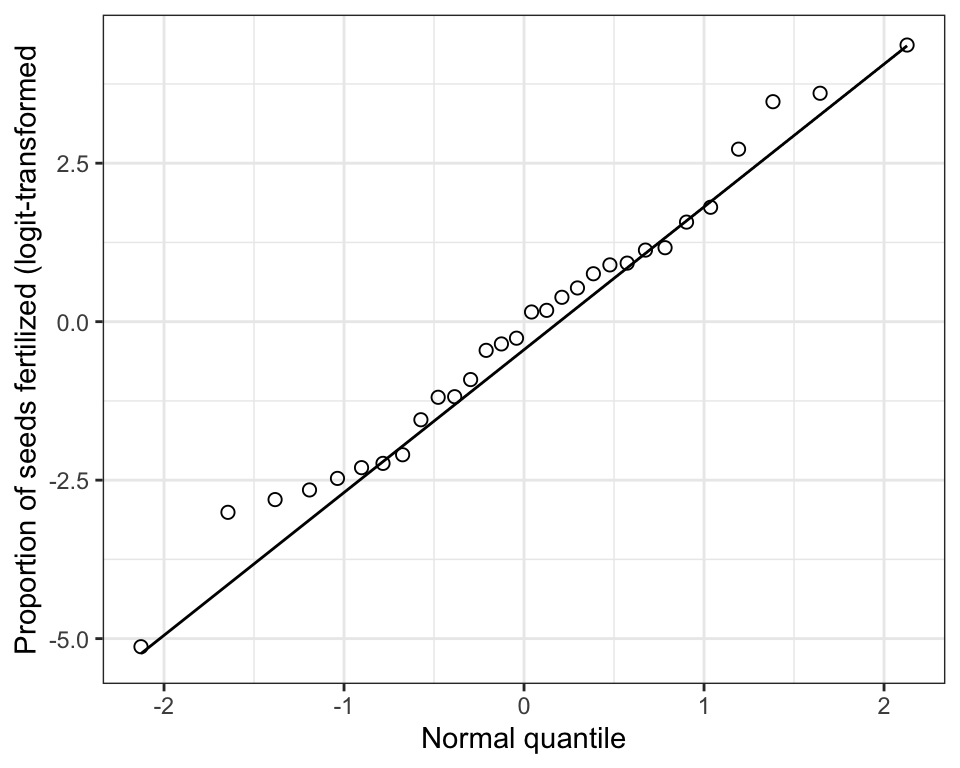
Figure 15.8: Normal quantile plot of made-up biomass data, log-transformed.
That’s a bit better. We would now use this new variable in our analyses (assuming it meets the normality assumption).
15.4.3 Log bases
The log function calculates the natural logarithm (base e), but related functions permit any base:
?logFor instance, log10 uses log base 10:
## # A tibble: 32 × 3
## biomassRatio logbiomass log10biomass
## <dbl> <dbl> <dbl>
## 1 1.34 0.2927 0.1271
## 2 1.96 0.6729 0.2923
## 3 2.49 0.9123 0.3962
## 4 1.27 0.2390 0.1038
## 5 1.19 0.1740 0.07555
## 6 1.15 0.1398 0.06070
## 7 1.29 0.2546 0.1106
## 8 1.05 0.04879 0.02119
## 9 1.1 0.09531 0.04139
## 10 1.21 0.1906 0.08279
## # ℹ 22 more rowsOr the alternative code:
marine$log10biomass <- log10(marine$biomassRatio)15.4.4 Back-transforming log data
In order to back-transform data that were transformed using the natural logarithm (log), you make use of the exp function:
?expLet’s try it, creating a new variable in the “marine” dataset so we can compare to the original “biomassRatio” variable:
First, back-transform the data and store the results in a new variable within the data frame:
Now have a look at the first few lines of the tibble (selecting the original “biomassRatio” and new “back_biomass” variables) to see if the data values are identical, as they should be:
## # A tibble: 32 × 2
## biomassRatio back_biomass
## <dbl> <dbl>
## 1 1.34 1.34
## 2 1.96 1.96
## 3 2.49 2.49
## 4 1.27 1.27
## 5 1.19 1.19
## 6 1.15 1.15
## 7 1.29 1.29
## 8 1.05 1.05
## 9 1.1 1.1
## 10 1.21 1.21
## # ℹ 22 more rowsYup, it worked!
If you had added a 1 to your variable prior to log-transforming, then the code would be:
marine <- marine %>%
mutate(back_biomass = exp(logbiomass) - 1)Notice the minus 1 comes after the exp function is executed.
If you had used the log base 10 transformation, then the code to back-transform is as follows:
## [1] 1.34 1.96 2.49 1.27 1.19 1.15 1.29 1.05 1.10 1.21 1.31 1.26 1.38 1.49 1.84
## [16] 1.84 3.06 2.65 4.25 3.35 2.55 1.72 1.52 1.49 1.67 1.78 1.71 1.88 0.83 1.16
## [31] 1.31 1.40The ^ symbol stands for “exponent”. So here we’re calculating 10 to the exponent x, where x is each value in the dataset.
15.4.5 Logit transform
Variables whose data represent proportions or percentages are, by definition, not drawn from a normal distribution: they are bound by 0 and 1 (or 0 and 100%). They should therefore be logit-transformed.
The boot package includes both the logit function and the inv.logit function, the latter for back-transforming.
However, the logit function that is in the car package is better, because it accommodates the possibility that your dataset includes a zero and / or a one (equivalently, a zero or 100 percent), and has a mechanism to deal with this properly.
The logit function in the boot package does not deal with this possibility for you.
However, the car package does not have a function that will back-transform logit-transformed data.
This is why we’ll use the logit function from the car package, and the inv.logit function from the boot package!
Let’s see how it works with the flowers dataset, which includes a variable propFertile that describes the proportion of seeds produced by individual plants that were fertilized.
Let’s visualize the data with a normal quantile plot:
flowers %>%
ggplot(aes(sample = propFertile)) +
stat_qq(shape = 1, size = 2) +
stat_qq_line() +
ylab("Proportion of seeds fertilized") +
xlab("Normal quantile") +
theme_bw()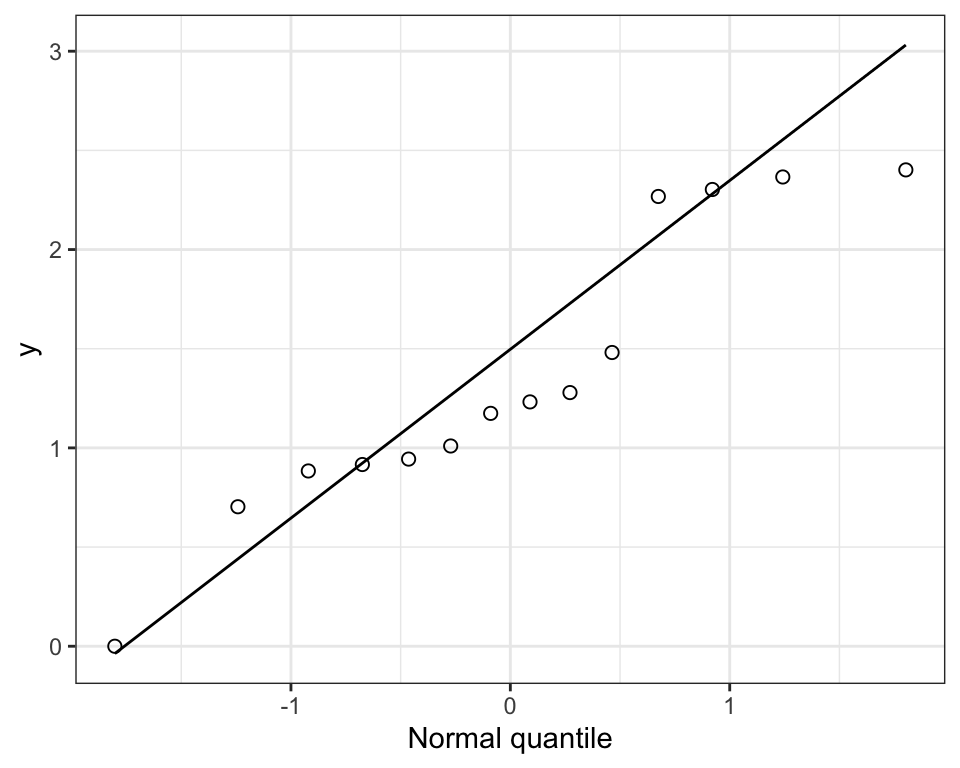
Figure 15.9: Normal quantile plot of the proportion of seeds fertilized on 30 plants (left) and the corresponding normal quantile plot (right)
Clearly not normal!
Now let’s logit-transform the data.
To ensure that we’re using the correct logit function, i.e. the one from the car package and NOT from the boot package, we can use the :: syntax, with the package name preceding the double-colons, which tells R the correct package to use.
Or the alternative code:
flowers$logitfertile <- car::logit(flowers$propFertile)Now let’s visualize the transformed data:
flowers %>%
ggplot(aes(sample = logitfertile)) +
stat_qq(shape = 1, size = 2) +
stat_qq_line() +
ylab("Proportion of seeds fertilized (logit-transformed") +
xlab("Normal quantile") +
theme_bw()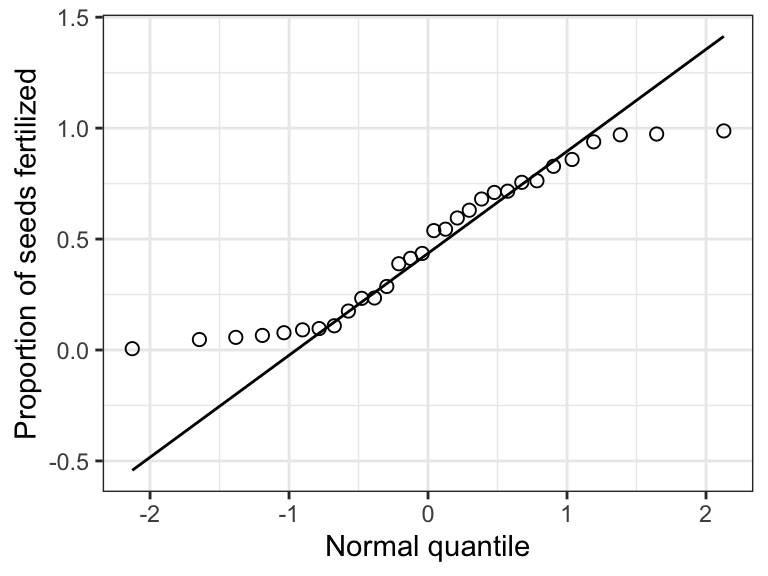
Figure 15.10: Normal quantile plot of the proportion of seeds fertilized (logit transformed) on 30 plants
That’s much better!
Next we learn how to back-transform logit data.
15.4.6 Back-transforming logit data
We’ll use the inv.logit function from the boot package:
?boot::inv.logitFirst do the back-transform:
Or alternative code:
flowers$flower_backtransformed <- boot::inv.logit(flowers$logitfertile)Let’s have a look at the original “propFertile” variable and the “flower_backtransformed” variable to check that they’re identical:
## # A tibble: 30 × 2
## propFertile flower_backtransformed
## <dbl> <dbl>
## 1 0.06571 0.06571
## 2 0.9874 0.9874
## 3 0.3888 0.3888
## 4 0.6805 0.6805
## 5 0.07781 0.07781
## 6 0.9735 0.9735
## 7 0.1755 0.1755
## 8 0.1092 0.1092
## 9 0.7158 0.7158
## 10 0.04708 0.04708
## # ℹ 20 more rowsYup, it worked!
15.4.7 When to back-transform?
You should back-transform your data when it makes sense to communicate findings on the original measurement scale.
The most common example is reporting confidence intervals for a mean or difference in means.
For example, imagine you had calculated a confidence interval for the log-transformed marine biomass ratio data, and your limits were as follows:
0.347 < \(ln(\mu)\) < 0.611
These are the log-transformed limits! So we need to back-transform them to get them in the original scale:
So now the back-transformed interval is:
1.415 < \(\mu\) < 1.842
Voila!