7.3 Describing a numerical variable

Numeric variables are described with measures of centre and spread.

Before calculating descriptive statistics for a numeric variable, it is advisable to visualize its frequency distribution first. Why? Because characteristics of the frequency distribution will govern which measures of centre and spread are more reliable or representative.

  • If the frequency distribution is roughly symmetric and does not have any obvious outliers, then the mean and the standard deviation are the preferred measures of centre and spread, respectively

  • If the frequency distribution is asymmetric and / or has outliers, the median and the inter-quartile range (IQR) are the preferred measures of centre and spread

It is often the case, however, that all four measures are presented together.

New tool Introducing the summarise function.

The dplyr package, which is loaded with the tidyverse, has a handy summarise (equivalently summarize) function for calculating descriptive statistics.

Check out its help file by copying the following code into your command console:

?summarise

Let’s use the penguins dataset for our demonstrations.

The first step is to visualize the frequency distribution. Given that this is a numeric variable, we do this using a histogram, as we learned in a previous tutorial.

ggplot(data = penguins, aes(x = body_mass_g)) +
  geom_histogram(binwidth = 500, colour = "black", fill = "lightgrey") +
  xlab("Body mass (g)") +
  ylab("Frequency") +
  theme_bw()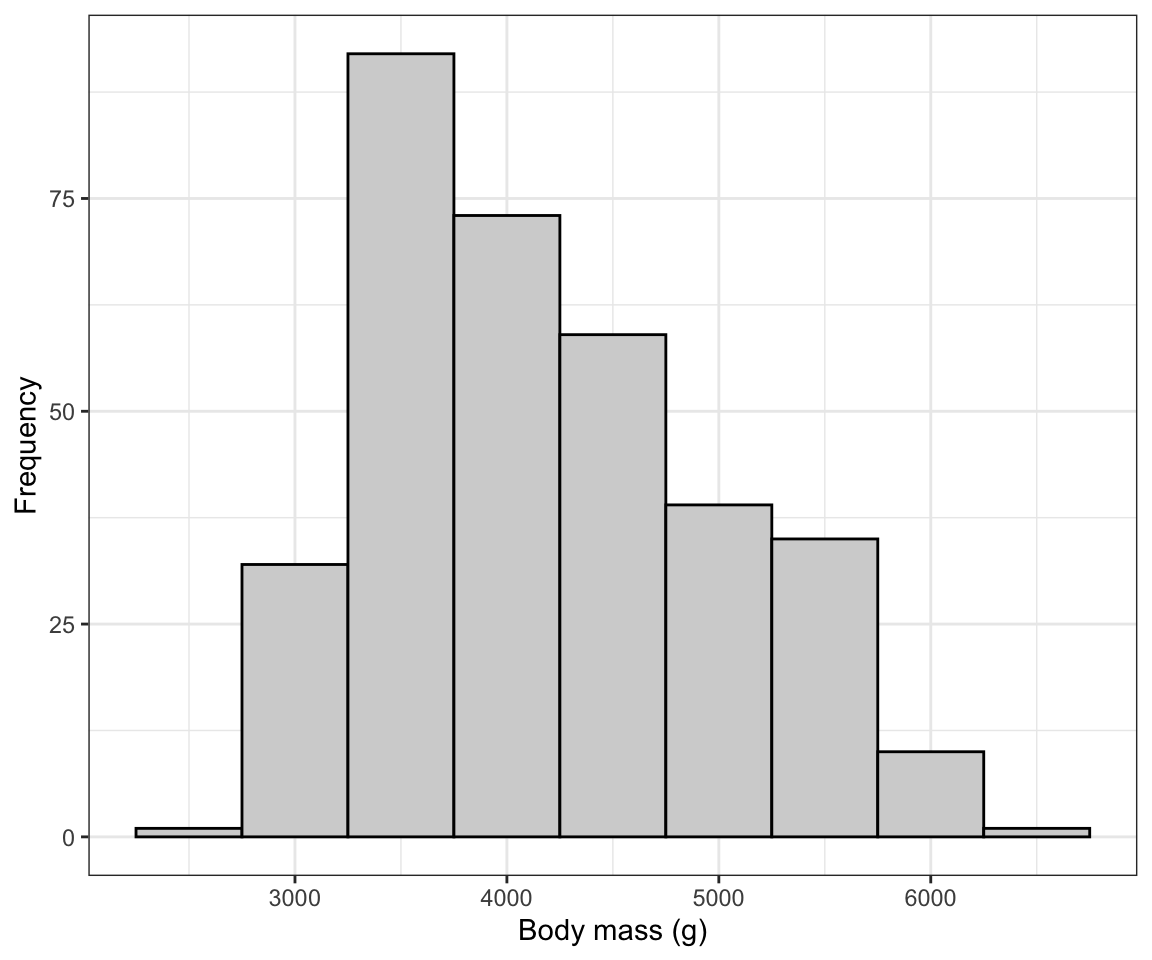
Histogram of body mass (g) for 342 penguins

Figure 7.1: Histogram of body mass (g) for 342 penguins

We are reminded that the distribution of body mass is moderately positively skewed and thus asymmetric, with a single mode near 3500g. There are no obvious outliers in the distribution.

This means that the median and IQR should be the preferred descriptors of centre and spread, respectively.

7.3.1 Calculating the median & IQR

So let’s calculate the median and IQR of body mass for all penguins. Let’s provide the code, then explain after:

penguins %>%
  summarise(
   median_body_mass_g =  median(body_mass_g),
   IQR_body_mass_g = IQR(body_mass_g)
    )

Uh oh! If you tried to run this code, it would have given you an error:

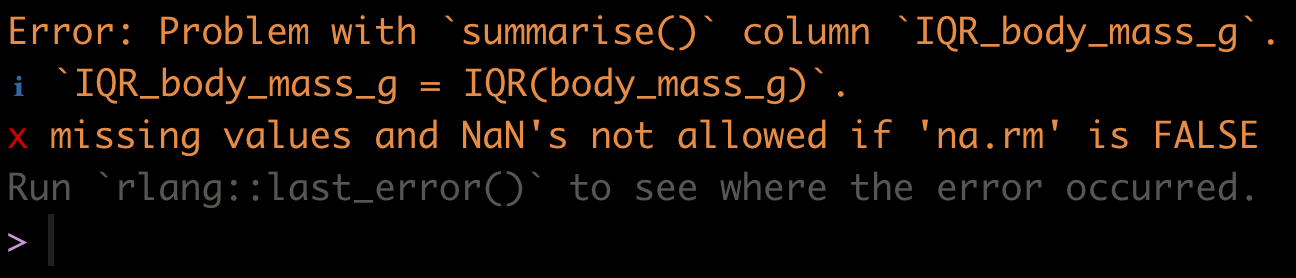
Error when functions encounter 'NA' values

Figure 7.2: Error when functions encounter ‘NA’ values

We forgot that when we previously got an overview of the penguins dataset we discovered there were missing values (“NA” values)!

TIP If there are “NA” values in the variable being analyzed, some R functions, such as the function median or mean, will simply return “NA”. To remedy this, we use the “na.rm = TRUE” argument.

Let’s try our code again, adding the “na.rm = TRUE” argument. And note that the key functions called within the summarise function are median and IQR (case sensitive!).

penguins %>%
  summarise(
   Median =  median(body_mass_g, na.rm = TRUE),
   InterQR = IQR(body_mass_g, na.rm = TRUE)
    )
## # A tibble: 1 × 2
##   Median InterQR
##    <dbl>   <dbl>
## 1   4050    1200

In the preceding code chunk, we have:

  • The name of the tibble (here penguins) being used in the subsequent functions
  • A pipe “%>% to tell R we’re not done coding
  • The summarise function (summarize will work too), telling R we’re going to calculate a new variable
  • The name we’ll give to the first variable we’re creating, here we call the variable “Median” (the “M” is capitalized to distinguish this variable name from the function median)
  • And we define how to calculate the “Median”, here using the median function
  • We feed the variable of interest from the penguins tibble, “body_mass_g”, to the median function, along with the argument “na.rm = TRUE”
  • We end the line with a comma, telling R that we’re not done providing arguments to the summarise function
  • We do the same for the inter-quartile range variable we’re creating called “InterQR”, calculating the value using the IQR function, and this time no comma at the end of the line, because this is the last argument being provided to the summarise function
  • We close out the parentheses for the summarise function

7.3.2 Calculating the mean & standard deviation

Although the median and IQR are the preferred descriptors for the body_mass_g variable, it is nonetheless commonplace to report the mean and standard deviation also.

Let’s do this, and while we’re at it, include even more descriptors to illustrate how they’re calculated.

This time we’ll put the output from our summarise function into a table, and then present it in a nice format, like we learned how to do for a frequency table.

Let’s create the table of descriptive statistics first, a tibble called “penguins.descriptors”, and we’ll describe what’s going on after (NOTE this code chunk was edited slightly on Sept. 30, 2021):

penguins.descriptors <- penguins %>%
  summarise( 
  Mean = mean(body_mass_g, na.rm = T),
  SD = sd(body_mass_g, na.rm = T),
  Median = median(body_mass_g, na.rm = T),
  InterQR = IQR(body_mass_g, na.rm = T),
  Count = n() - naniar::n_miss(body_mass_g),
  Count_NA = naniar::n_miss(body_mass_g))

The first 4 descriptive statistics are self-explanatory based on their variable names.

The last two: “Count” and “Count_NA” are providing the total number of complete observations in the body_mass_g variable (thus the number of observations that went into calculating the descriptive statistics), and then the total number of missing values (NAs) in the variable, respectively.

The last two lines of code above require further explanation:

This code: Count = n() - naniar::n_miss(body_mass_g)) tells R to first tally the total sample size using the n() function, then to subtract from that the total number of missing values, which is calculated using the n_miss function from the naniar package.

The double colons in naniar::n_miss(body_mass_g) indicates that the function n_miss comes from the naniar package. This syntax, which we have not used previously, provides a failsafe way to run a function even if the package is not presently loaded.

The same coding approach is used in the last line: Count_NA = naniar::n_miss(body_mass_g).

TIP It is important to calculate the total number of complete observations in the variable of interest, because, as described in the Biology Procedures and Guidelines document, this number needs to be reported in figure and table headings.

Now let’s show the table of descriptive statistics, using the kable function we learned about in a previous tutorial.

penguins.descriptors %>%
  kable(caption = "Descriptive statistics of measurements of body mass (g) for 342 penguins", digits = 3)
Table 7.2: Descriptive statistics of measurements of body mass (g) for 342 penguins
Mean SD Median InterQR Count Count_NA
4201.754 801.955 4050 1200 342 2

In another tutorial we’ll learn how to present the table following all the guidelines in the Biology Guidelines and Procedures document, including, for example, significant digits. For now, the preceding table is good!

  1. Descriptive statistics: Create a histogram and table of descriptive statistics for the “flipper_length_mm” variable in the penguins dataset.