14.2 Paired t-test

We’ll use the blackbird dataset for this example.

For 13 red-winged blackbirds, measurements of antibodies were taken before and after implantation with testosterone. Thus, the same bird was measured twice. Clearly, these measurements are not independent, hence the need for a “paired” t-test.

Let’s first have a look at the blackbird dataset:

blackbird 
## # A tibble: 26 × 3
##    blackbird time   Antibody
##        <dbl> <chr>     <dbl>
##  1         1 Before    4.654
##  2         2 Before    3.912
##  3         3 Before    4.913
##  4         4 Before    4.500
##  5         5 Before    4.804
##  6         6 Before    4.883
##  7         7 Before    4.875
##  8         8 Before    4.779
##  9         9 Before    4.977
## 10        10 Before    4.868
## # ℹ 16 more rows

The data frame has 26 rows, and includes 3 variables, the first of which “blackbird” simply keeps track of the individual ID of blackbirds.

The response variable of interest, “Antibody” represents antibody production rate measured in units of natural logarithm (ln) 10^{-3} optical density per minute (ln[mOD/min]).

The factor variable time that has two levels: “After” and “Before”.

These data are stored in tidy format, which, as you’ve learned, is the ideal format for storing data.

Sometimes you may get data in wide format, in which case, for instance, we would have a column for the “Before” antibody measurements and another column for the “After” measurements.

It is always preferable to work with long-format (tidy) data.

Consult the following webpage for instructions on using the tidyr package for converting between wide and long data formats.

With our data in the preferred long format, we can proceed with our hypothesis test, but because the hypothesis focuses on the differences in the paired measurements, we need to calculate those first!

14.2.1 Calculate differences

Let’s remind ourselves how the data are stored:

blackbird
## # A tibble: 26 × 3
##    blackbird time   Antibody
##        <dbl> <chr>     <dbl>
##  1         1 Before    4.654
##  2         2 Before    3.912
##  3         3 Before    4.913
##  4         4 Before    4.500
##  5         5 Before    4.804
##  6         6 Before    4.883
##  7         7 Before    4.875
##  8         8 Before    4.779
##  9         9 Before    4.977
## 10        10 Before    4.868
## # ℹ 16 more rows

We’ll use, for the first time, the pivot_wider function from the dplyr package (which is loaded as part of the tidyverse).

The pivot_wider function essentially takes data stored in long format and converts it to wide format.

The following code requires that there be at least one variable in the tibble that provides a unique identifier for each individual. In the “blackbird” tibble, this variable is “blackbird”. I have added an argument “id_cols = blackbird” to the code below to underscore the need for this type of identifier variable. The code will not work if such a variable does not exist in the tibble.

Here’s the code, then we’ll explain after:

blackbird.diffs <- blackbird %>%
  pivot_wider(id_cols = blackbird, names_from = time, values_from = Antibody) %>%
  mutate(diffs = After - Before)

In the preceding chunk, we:

  • create a new object “blackbird.diffs” to hold our data
  • the pivot_wider function takes the following arguments:
    • “id_cols = blackbird”, which tells the function which variable in the tibble is used to keep track of the unique individuals (here, the “blackbird” variable)
    • A categorical (grouping) variable “names_from” and creates new columns, one for each unique category
    • A “values_from” variable; thus, in our case, we get 2 new columns (because there are 2 categories to the “time” variable: Before and After), and the values placed in those columns are the corresponding values of “Antibody”.
  • we then create a new variable “diff” that equals the values in the newly created “After” variable minus the values in the “Before” variable.

TIP: In the blackbird example we have “Before” and “After” measurements of a variable, and we calculated the difference as “\(After - Before\)”, as this is a logical way to do it. It doesn’t really matter which direction you calculate the difference, but just be aware that you need to make clear how it was calculated, so that your interpretation is correct.

Let’s have a look at the result:

blackbird.diffs
## # A tibble: 13 × 4
##    blackbird Before After    diffs
##        <dbl>  <dbl> <dbl>    <dbl>
##  1         1  4.654 4.443 -0.2113 
##  2         2  3.912 4.304  0.3920 
##  3         3  4.913 4.977  0.06408
##  4         4  4.500 4.454 -0.04546
##  5         5  4.804 4.997  0.1932 
##  6         6  4.883 4.997  0.1144 
##  7         7  4.875 5.011  0.1354 
##  8         8  4.779 4.956  0.1767 
##  9         9  4.977 5.017  0.04055
## 10        10  4.868 4.727 -0.1401 
## 11        11  4.754 4.771  0.01709
## 12        12  4.700 4.595 -0.1054 
## 13        13  4.927 5.011  0.08338

We can see that some of the diffs values are negative, and some are positive. These would of course be switched in sign if we had calculated the differences as “\(Before - After\)”.

In any case, this is the new tibble and variable “diffs” that we’ll use for our hypothesis test!

14.2.2 Hypothesis statement

The hypotheses for this paired t-test focus on the mean of the differences between the paired measurements, denoted by \(\mu_d\):

H0: The mean change in antibody production after testosterone implants was zero (\(\mu_d = 0\)).
HA: The mean change in antibody production after testosterone implants was not zero (\(\mu_d \neq 0\)).

Steps to a hypothesis test:

  • We’ll use an \(\alpha\) level of 0.05.
  • It is a two-tailed alternative hypothesis
  • We’ll visualize the data, and interpret the output
  • We’ll use a paired t-test test to test the null hypothesis, because we’re dealing with “before and after” measurements taken on the same individuals, and drawing inferences about a population mean \(\mu_d\) using sample data
  • We’ll check the assumptions of the test (see below)
  • We’ll calculate our test statistic
  • We’ll calculate the P-value associated with our test statistic
  • We’ll calculate a 95% confidence interval for the mean difference
  • We’ll provide a good concluding statement that includes a 95% confidence interval for the mean difference

14.2.3 A graph to accompany a paired t-test

The best way to visualize the data for a paired t-test is to create a histogram of the calculated differences between the paired observations.

blackbird.diffs %>% 
  ggplot(aes(x = diffs)) +
  geom_histogram(binwidth = 0.1, boundary = -0.3, 
                 color = "black", fill = "lightgrey",) +
  xlab("Difference in antibody production rate (after - before) (ln[mOD/min]) 10^-3") +
  ylab("Frequency") +
  theme_bw()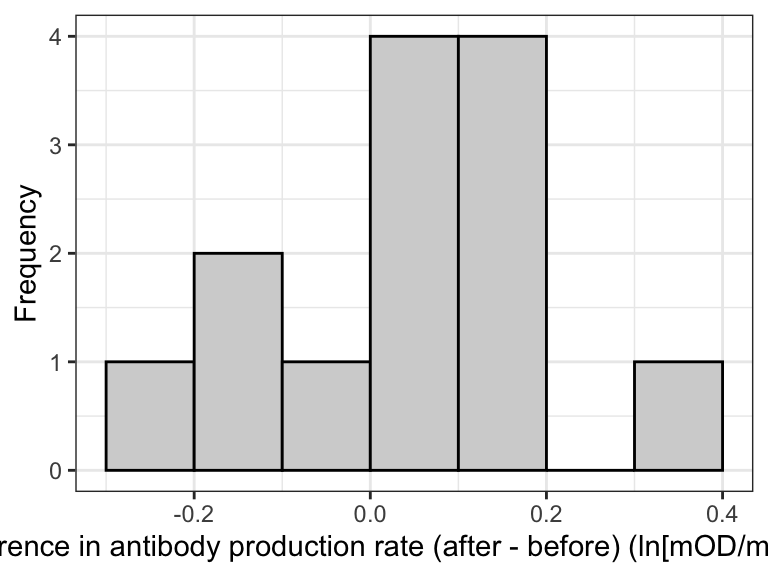
Histogram of the differences in antibody production rate before and after the testosterone treatment

Figure 14.1: Histogram of the differences in antibody production rate before and after the testosterone treatment

With such a small sample size (13), the histogram is not particularly informative. But we do see most observations are just above zero.

OPTIONAL

Another optional but nice way to visualize paired data is using a paired plot.

blackbird %>%
  ggplot(aes(x = time, y = Antibody)) +
  geom_point(shape = 1, size = 1.5) +
  geom_line(aes(group = blackbird), color = "grey") +
  theme_bw()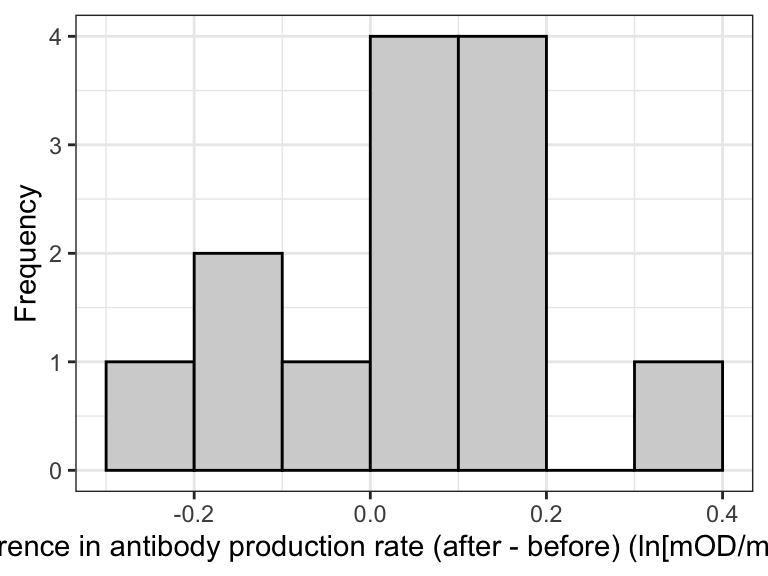
Paired plot of antibody production rate before and after the testosterone treatment

Figure 14.2: Paired plot of antibody production rate before and after the testosterone treatment

OPTIONAL

Notice that the “After” group is plotted on the left, which is a bit counter-intuitive. We could optionally change that by changing how R recognizes the “order” of the “time” variable:

blackbird$time <- ordered(blackbird$time, levels = c("Before", "After"))

Then repeat the code above to create the paired plot.

14.2.4 Assumptions of the paired t-test

(Updated October 31, 2024)

The assumptions of the paired t-test are the same as the assumptions for the one-sample t-test, except they pertain to the difference:

  • the sampling units are randomly sampled from the population
  • the mean difference has a normal distribution in the population (each group of measurements need not be normally distributed)

As instructed in the checking assumptions tutorial, we should use a normal quantile plot to visually check the normal distribution assumption, using the calculated differences.

blackbird.diffs %>%
  ggplot(aes(sample = diffs)) +
  stat_qq(shape = 1, size = 2) +
  stat_qq_line() +
  xlab("Normal quantile") +
  ylab("Antibody production (ln[mOD/min]) 10^-3") +
  theme_bw()
Normal quantile plot of the differences in antibody production rate before and after the testosterone treatment (ln[mOD/min]) 10^-3.

Figure 14.3: Normal quantile plot of the differences in antibody production rate before and after the testosterone treatment (ln[mOD/min]) 10^-3.

We see that most of the lines are close to the line, with one point near the top right that is a bit off…

A reasonable statement would be:

“The normal quantile plot shows that the data generally fall close to the line (except perhaps the highest value), indicating that the normality assumption is reasonably met.”

But if you’re feeling uncertain, we can follow this with a Shapiro-Wilk Normality Test, which tests the null hypothesis that the data are sampled from a normal distribution.

shapiro.result <- shapiro.test(blackbird.diffs$diffs)
shapiro.result.tidy <- tidy(shapiro.result)
shapiro.result.tidy
## # A tibble: 1 × 3
##   statistic p.value method                     
##       <dbl>   <dbl> <chr>                      
## 1    0.9781  0.9688 Shapiro-Wilk normality test

Given that the P-value is large (and much greater than 0.05), there is no reason to reject the null hypothesis. Thus, our normality assumption is met.

When testing the normality assumption using the Shapiro-Wilk test, there is no need to conduct all the steps associated with a hypothesis test. Simply report the results of the test (the test statistic value and the associated P-value).

For instance:

“A Shapiro-Wilk test revealed no evidence against the assumption that the data are drawn from a normal distribution (W = 0.98, P-value = 0.969).”

14.2.5 Conduct the test

We can conduct a paired t-test in two different ways:

  • conduct a one-sample t-test on the differences using the t.test function and methods you learned in a previous tutorial.

  • conduct a paired t-test using the t.test function and the argument paired = TRUE.

(1) One-sample t-test on the differences

Let’s proceed with the test as we’ve previously learned.

Here we make sure to set the null hypothesized value of “mu” to zero in the argument for the t.test function:

blackbird.ttest <- blackbird.diffs %>%
  select(diffs) %>%
  t.test(mu = 0, alternative = "two.sided", conf.level = 0.95)

Now have a look at the result:

blackbird.ttest
## 
##  One Sample t-test
## 
## data:  .
## t = 1.2435, df = 12, p-value = 0.2374
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.04134676  0.15128638
## sample estimates:
##  mean of x 
## 0.05496981

The observed P-value for our test is larger than our \(\alpha\) level of 0.05. We therefore fail to reject the null hypothesis.

The values of t and of the lower and upper confidence limits may be reversed in sign, if you conducted your calculation of differences in the alternative way. Specifically, you may get t = -1.2434925, and confidence limits of -0.1512864 and 0.0413468. This is totally fine!

(2) Paired t-test

(Updated October 31, 2024)

Here again we’ll use the wide-format tibble blackbird.diffs, using this approach:

blackbird.paired.ttest <- t.test(x = blackbird.diffs$Before, y = blackbird.diffs$After,
       paired = TRUE, alternative = 'two.sided', conf.level = 0.95)

Here’s an explanation:

  • we create a new object “blackbird.paried.ttest” to store our results in
  • we run the t.test function with the arguments as follows:
    • we specify x equal to the “Before” variable, and y equal to the “After” variable
    • we have the “paired = TRUE” argument, telling the function that this is a paired design
    • we specify that this is a two-sided test with “alternative = ‘two.sided’
    • finally we use “conf.level = 0.95” which corresponds to an \(\alpha = 0.05\)

Let’s look at the result:

blackbird.paired.ttest
## 
##  Paired t-test
## 
## data:  blackbird.diffs$Before and blackbird.diffs$After
## t = -1.2435, df = 12, p-value = 0.2374
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -0.15128638  0.04134676
## sample estimates:
## mean difference 
##     -0.05496981

The output is identical to what we got when we applied a 1-sample t-test on the differences!

The values of t and of the lower and upper confidence limits may be reversed in sign, if you conducted your calculation of differences in the alternative way. Specifically, you may get t = -1.2434925, and confidence limits of -0.1512864 and 0.0413468. This is totally fine!

14.2.6 Concluding statement

Here’s an example of a reasonable concluding statement, and this can apply for either of the two methods used above (note that in either case we call the test a “paired t-test, even if we used the one-sample t-test on the differences):

We have no reason to reject the null hypothesis that the mean change in antibody production after testosterone implants was zero (paired t-test; t = -1.24; df = 12; P = 0.237; 95% confidence interval for the difference: -0.151 \(< \mu_d <\) 0.041).