17.2 Pearson correlation analysis

It is commonplace in biology to wish to quantify the strength and direction of a linear association between two numerical variables.

For example, in an earlier tutorial we visualized the association between bill depth and bill length among Adelie penguins, using the “penguins” dataset. Here we learn how to quantify the strength and direction of this type of association by calculating the Pearson correlation coefficient.

When drawing inferences about associations between numerical variables in a population, the true correlation coefficient is referred to as “rho” or \(\rho\).

The sample-based correlation coefficient, which we use to estimate \(\rho\), is referred to as \(r\):

\[r = \frac{\sum{(X_{i}-\bar{X})(Y_{i}-\bar{Y})}}{\sqrt{\sum{(X_{i}-\bar{X})^2}} {\sqrt{\sum(Y_{i}-\bar{Y})^2}}}\]

In the calculation of \(r\) it does not matter which variable is treated as the \(X\) and which as the \(Y\). However, in many instances there may good reason to choose which serves as the \(X\) (explanatory) and which as the \(Y\) (response).

17.2.1 Hypothesis statements

As a refresher, first consult the steps to hypothesis testing.

Researchers were interested in whether inbreeding coefficients of the wolf litters were associated with the number of pups surviving their first winter.

Both variables are numerical, and so the first choice is to conduct a Pearson correlation analysis. This analysis yields a sample-based measure called Pearson’s correlation coefficient, or r. This provides an estimate of \(\rho\) - the true correlation between the two variables in the population. The absolute magnitude of r (and \(\rho\)) reflects the strength of the linear association between two numeric variables in the population, and the sign of the coefficient indicates the direction of the association.

The hypothesis statements should be framed in the context of the question, and should include the hypothesized value of the population parameter.

H₀: Inbreeding coefficients are not associated with the number of pups surviving the first winter (\(\rho = 0\)). H_A: Inbreeding coefficients are associated with the number of pups surviving the first winter (\(\rho \ne 0\)).

We’ll set \(\alpha\) = 0.05.

17.2.2 Visualize the data

We learned in an earlier tutorial that the best way to visualize an association between two numeric variables is with a scatterplot, and that we can create a scatterplot using the geom_point function from the ggplot2 package:

wolf %>% 
ggplot(aes(x = nPups, y = inbreedCoef)) +
  geom_point(shape = 1) +
  xlab("Number of pups") +
  ylab("Inbreeding coefficient") +
  theme_bw()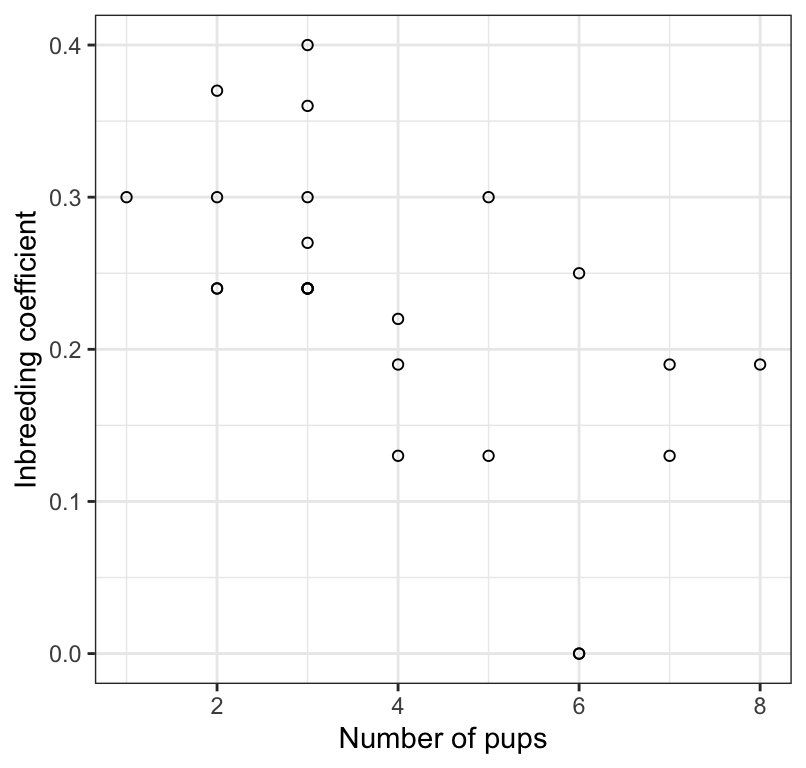

Figure 17.1: The association between inbreeding coefficient and number of surviving wolf pups (n = 24).

We notice that there doesn’t appear to be the correct number of points (24) in the scatterplot, so there must be some overlapping.

To remedy this, we use the geom_jitter function instead of the geom_point function.

wolf %>% 
ggplot(aes(x = nPups, y = inbreedCoef)) +
  geom_jitter(shape = 1) +
  xlab("Number of pups") +
  ylab("Inbreeding coefficient") +
  theme_bw()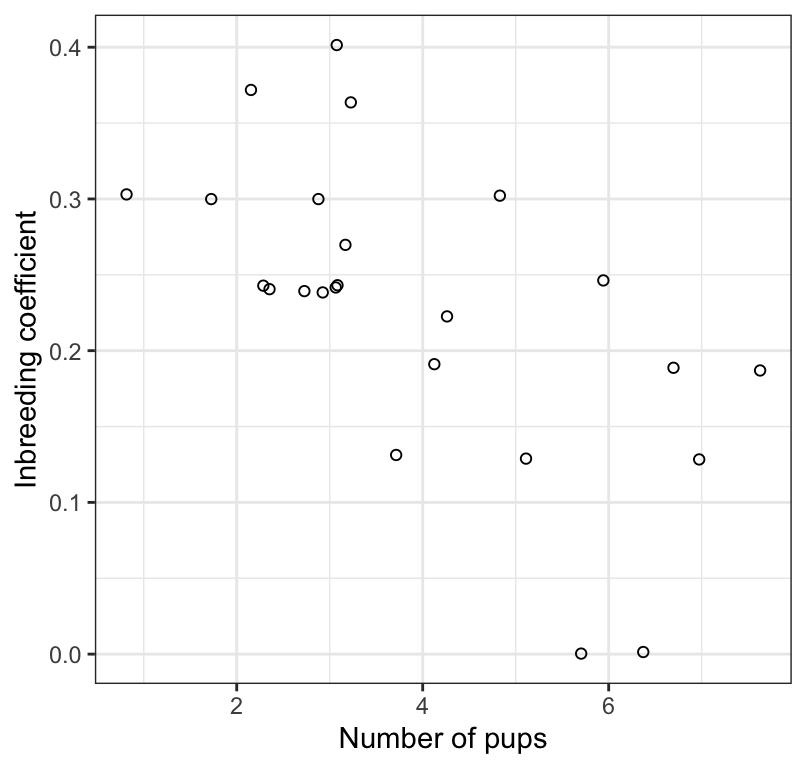

The association between inbreeding coefficient and number of surviving wolf pups (n = 24). Values have been jittered slightly to improve legibility.

Figure 17.2: The association between inbreeding coefficient and number of surviving wolf pups (n = 24). Values have been jittered slightly to improve legibility.

That’s better!

Interpreting a scatterplot

In an earlier tutorial, we learned how to properly interpret a scatterplot, and what information should to include in your interpretation. Be sure to consult that tutorial.

We see in Figure 17.2 that the association between the inbreeding coefficient and number of surviving pups is negative, linear, and moderately strong. There are no apparent outliers to the association.

17.2.3 Assumptions of correlation analysis

Correlation analysis assumes that:

the sample of individuals is a random sample from the population
the measurements have a bivariate normal distribution, which includes the following properties:
- the relationship between the two variables (\(X\) and \(Y\)) is linear
- the cloud of points in a scatterplot of \(X\) and \(Y\) has a circular or elliptical shape
- the frequency distributions of \(X\) and \(Y\) separately are normal

Checking the assumptions of correlation analysis

The assumptions are most easily checked using the scatterplot of X and Y.

What to look for as potential problems in the scatterplot:

a “funnel” shape
outliers to the general trend
non-linear association

If any of these patterns are evident, then one should opt for a non-parametric analysis (see below).

(See Figure 16.3-2 in the text for examples of non-conforming scatterplots)

Based on Figure 17.2, there doesn’t seem to be any indications that the assumptions are not met, so we’ll proceed with testing the null hypothesis.

Be careful with “count” type variables such as “number of pups”, as these may not adhere to the “bivariate normality” assumption. If the variable is restricted to a limited range of possible counts, say zero to 5 or 6, then the association should probably be analyzed using a non-parametric test (see below). The variable “number of pups” in this example is borderline OK…

17.2.4 Conduct the correlation analysis

Conducting a correlation analysis is done using the cor.test function that comes with R.

This function does not produce “tidy” output, so we’ll make use of the tidy function from the broom package to tidy up the correlation output (like we did in for ANOVA output).

Notice that the function expects the “x” and “y” variables as separate arguments.

And here’s how to implement it. First run the cor.test function, and notice we provide the “x” and “y” variables

wolf.cor <- cor.test(x = wolf$inbreedCoef, y = wolf$nPups, 
                     method = "pearson", conf.level = 0.95,
                     alternative = "two.sided")

Let’s have a look at the untidy output:

wolf.cor

## 
##  Pearson's product-moment correlation
## 
## data:  wolf$inbreedCoef and wolf$nPups
## t = -3.5893, df = 22, p-value = 0.001633
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.8120418 -0.2706791
## sample estimates:
##        cor 
## -0.6077184

Now let’s tidy it up and have a look at the resulting tidy output:

wolf.cor.tidy <- wolf.cor %>%
  broom::tidy()

Show the output:

wolf.cor.tidy

## # A tibble: 1 × 8
##   estimate statistic  p.value parameter conf.low conf.high method    alternative
##      <dbl>     <dbl>    <dbl>     <int>    <dbl>     <dbl> <chr>     <chr>      
## 1  -0.6077    -3.589 0.001633        22  -0.8120   -0.2707 Pearson'… two.sided

The “estimate” value represents the value of Pearson’s correlation coefficient \(r\)
The “statistic” value is actually the value for \(t\), which is used to test the significance of r
The “p.value” associated with the observed value of t
The “parameter” value is, strangely, referring to the degrees of freedom for the test, \(df = n - 2\)
The output also includes the confidence interval for r (“conf.low” and “conf.high”)
The “method” refers to the type of test conducted
The “alternative” indicates whether the alternative hypothesis was one- or two-sided (the latter is the default)

Despite the reporting of the t test statistic, we do not report t in our concluding statement (see below).

17.2.5 Concluding statement

It is advisable to always refer to a scatterplot when authoring a concluding statement for correlation analysis.

Let’s re-do the scatterplot here.

wolf %>% 
ggplot(aes(x = nPups, y = inbreedCoef)) +
  geom_jitter(shape = 1) +
  xlab("Number of pups") +
  ylab("Inbreeding coefficient") +
  theme_bw()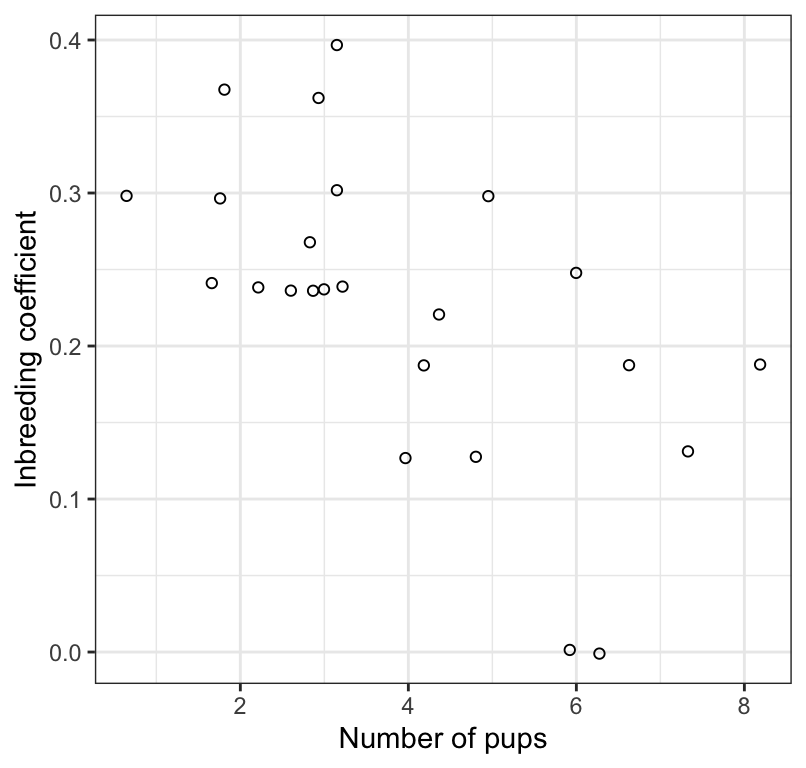

Figure 17.3: The association between inbreeding coefficient and number of surviving wolf pups (n = 24). Values have been jittered slightly to improve legibility.

Here is an example of a good concluding statement:

Litter size is significantly negatively correlated with the inbreeding coefficient of the parents (Figure 17.3; Pearson r = -0.61; 95% confidence limits: -0.812, -0.271; \(df\) = 22; P = 0.002).

Tip Remember to double-check if you had any missing values in your dataset, do that you don’t report the wrong sample size in your figure caption and / or concluding statement.

Using the penguins dataset that loads with the palmerpenguins package, test the null hypothesis that there is no linear association between bill length and bill depth among Gentoo penguins. HINT: Before using the cor.test function, you’ll first need to create a new tibble that includes only the “Gentoo” species data.